Назначение сервиса . Матричный калькулятор предназначен для решения систем линейных уравнений матричным способом (см. пример решения подобных задач).

Инструкция . Для онлайн решения необходимо выбрать вид уравнения и задать размерность соответствующих матриц.

Вид уравнения : A·X = B X·A = B A·X·B = C
Размерность матрицы А
Размерность матрицы B 1 2 3 4 5 6 7 8 9 10 x 1 2 3 4 5 6 7 8 9 10

Размерность матрицы C 1 2 3 4 5 6 7 8 9 10 x 1 2 3 4 5 6 7 8 9 10

где А, В, С - задаваемые матрицы, Х - искомая матрица. Матричные уравнения вида (1), (2) и (3) решаются через обратную матрицу A -1 . Если задано выражение A·X - B = C , то необходимо, сначала сложить матрицы C + B , и находить решение для выражения A·X = D , где D = C + B (). Если задано выражение A*X = B 2 , то предварительно матрицу B надо возвести в квадрат . Рекомендуется также ознакомиться с основными действиями над матрицами .

Пример №1 . Задание . Найти решение матричного уравнения
Решение . Обозначим:
Тогда матричное уравнение запишется в виде: A·X·B = C.
Определитель матрицы А равен detA=-1
Так как A невырожденная матрица, то существует обратная матрица A -1 . Умножим слева обе части уравнения на A -1:Умножаем обе части этого равенства слева на A -1 и справа на B -1: A -1 ·A·X·B·B -1 = A -1 ·C·B -1 . Так как A·A -1 = B·B -1 = E и E·X = X·E = X, то X = A -1 ·C·B -1

Обратная матрица A -1:
Найдем обратную матрицу B -1 .
Транспонированная матрица B T:
Обратная матрица B -1:
Матрицу X ищем по формуле: X = A -1 ·C·B -1

Ответ:

Пример №2 . Задание. Решить матричное уравнение
Решение . Обозначим:
Тогда матричное уравнение запишется в виде: A·X = B.
Определитель матрицы А равен detA=0
Так как A вырожденная матрица (определитель равен 0), следовательно уравнение решения не имеет.

Пример №3 . Задание. Найти решение матричного уравнения
Решение . Обозначим:
Тогда матричное уравнение запишется в виде: X·A = B.
Определитель матрицы А равен detA=-60
Так как A невырожденная матрица, то существует обратная матрица A -1 . Умножим справа обе части уравнения на A -1: X·A·A -1 = B·A -1 , откуда находим, что X = B·A -1
Найдем обратную матрицу A -1 .
Транспонированная матрица A T: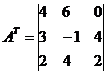
Обратная матрица A -1:
Матрицу X ищем по формуле: X = B·A -1


Ответ: >

Уравнения

Как решать уравнения?

В этом разделе мы вспомним (или изучим – уж кому как) самые элементарные уравнения. Итак, что такое уравнение? Говоря человеческим языком, это какое-то математическое выражение, где есть знак равенства и неизвестное. Которое, обычно, обозначается буквой «х» . Решить уравнение - это найти такие значения икса, которые при подстановке в исходное выражение, дадут нам верное тождество. Напомню, что тождество – это выражение, которое не вызывает сомнения даже у человека, абсолютно не отягощенного математическими знаниями. Типа 2=2, 0=0, ab=ab и т.д. Так как решать уравнения? Давайте разберёмся.

Уравнения бывают всякие (вот удивил, да?). Но всё их бесконечное многообразие можно разбить всего на четыре типа.

4. Все остальные.)

Всех остальных, разумеется, больше всего, да...) Сюда входят и кубические, и показательные, и логарифмические, и тригонометрические и всякие другие. С ними мы в соответствующих разделах плотно поработаем.

Сразу скажу, что иногда и уравнения первых трёх типов так накрутят, что и не узнаешь их… Ничего. Мы научимся их разматывать.

И зачем нам эти четыре типа? А затем, что линейные уравнения решаются одним способом, квадратные другим, дробные рациональные - третьим, а остальные не решаются вовсе! Ну, не то, чтобы уж совсем никак не решаются, это я зря математику обидел.) Просто для них существуют свои специальные приёмы и методы.

Но для любых (повторяю - для любых! ) уравнений есть надёжная и безотказная основа для решения. Работает везде и всегда. Эта основа - Звучит страшно, но штука очень простая. И очень (очень!) важная.

Собственно, решение уравнения и состоит из этих самых преобразований. На 99%. Ответ на вопрос: "Как решать уравнения? " лежит, как раз, в этих преобразованиях. Намёк понятен?)

Тождественные преобразования уравнений.

В любых уравнениях для нахождения неизвестного надо преобразовать и упростить исходный пример. Причем так, чтобы при смене внешнего вида суть уравнения не менялась. Такие преобразования называются тождественными или равносильными.

Отмечу, что эти преобразования относятся именно к уравнениям. В математике ещё имеются тождественные преобразования выражений. Это другая тема.

Сейчас мы с вами повторим все-все-все базовые тождественные преобразования уравнений.

Базовые потому, что их можно применять к любым уравнениям – линейным, квадратным, дробным, тригонометрическим, показательным, логарифмическим и т.д. и т.п.

Первое тождественное преобразование: к обеим частям любого уравнения можно прибавить (отнять) любое (но одно и то же!) число или выражение (в том числе и выражение с неизвестным!). Суть уравнения от этого не меняется.

Вы, между прочим, постоянно пользовались этим преобразованием, только думали, что переносите какие-то слагаемые из одной части уравнения в другую со сменой знака. Типа:

Дело знакомое, переносим двойку вправо, и получаем:

На самом деле вы отняли от обеих частей уравнения двойку. Результат получается тот же самый:

х+2 - 2 = 3 - 2

Перенос слагаемых влево-вправо со сменой знака есть просто сокращённый вариант первого тождественного преобразования. И зачем нам такие глубокие познания? – спросите вы. В уравнениях низачем. Переносите, ради бога. Только знак не забывайте менять. А вот в неравенствах привычка к переносу может и в тупик поставить….

Второе тождественное преобразование : обе части уравнения можно умножить (разделить) на одно и то же отличное от нуля число или выражение. Здесь уже появляется понятное ограничение: на ноль умножать глупо, а делить и вовсе нельзя. Это преобразование вы используете, когда решаете что-нибудь крутое, типа

Понятное дело, х = 2. А вот как вы его нашли? Подбором? Или просто озарило? Чтобы не подбирать и не ждать озарения, нужно понять, что вы просто поделили обе части уравнения на 5. При делении левой части (5х) пятёрка сократилась, остался чистый икс. Чего нам и требовалось. А при делении правой части (10) на пять, получилась, знамо дело, двойка.

Вот и всё.

Забавно, но эти два (всего два!) тождественных преобразования лежат в основе решения всех уравнений математики. Во как! Имеет смысл посмотреть на примерах, что и как, правда?)

Примеры тождественных преобразований уравнений. Основные проблемы.

Начнём с первого тождественного преобразования. Перенос влево-вправо.

Пример для младшеньких.)

Допустим, надо решить вот такое уравнение:

3-2х=5-3х

Вспоминаем заклинание: "с иксами - влево, без иксов - вправо!" Это заклинание - инструкция по применению первого тождественного преобразования.) Какое выражение с иксом у нас справа? 3х ? Ответ неверный! Справа у нас - 3х ! Минус три икс! Стало быть, при переносе влево, знак поменяется на плюс. Получится:

3-2х+3х=5

Так, иксы собрали в кучку. Займёмся числами. Слева стоит тройка. С каким знаком? Ответ "с никаким" не принимается!) Перед тройкой, действительно, ничего не нарисовано. А это значит, что перед тройкой стоит плюс. Так уж математики договорились. Ничего не написано, значит, плюс. Следовательно, в правую часть тройка перенесётся с минусом. Получим:

-2х+3х=5-3

Остались сущие пустяки. Слева - привести подобные, справа - посчитать. Сразу получается ответ:

В этом примере хватило одного тождественного преобразования. Второе не понадобилось. Ну и ладно.)

Пример для старшеньких.)

Если Вам нравится этот сайт...

Кстати, у меня есть ещё парочка интересных сайтов для Вас.)

Можно потренироваться в решении примеров и узнать свой уровень. Тестирование с мгновенной проверкой. Учимся - с интересом!)

можно познакомиться с функциями и производными.

I. ax 2 =0 – неполное квадратное уравнение (b=0, c=0 ). Решение: х=0. Ответ: 0.

Решить уравнения.

2x·(x+3)=6x-x 2 .

Решение. Раскроем скобки, умножив 2х на каждое слагаемое в скобках:

2x 2 +6x=6x-x 2 ; переносим слагаемые из правой части в левую:

2x 2 +6x-6x+x 2 =0; приводим подобные слагаемые:

3x 2 =0, отсюда x=0.

Ответ: 0.

II. ax 2 +bx=0 – неполное квадратное уравнение (с=0 ). Решение: x (ax+b)=0 → x 1 =0 или ax+b=0 → x 2 =-b/a. Ответ: 0; -b/a.

5x 2 -26x=0.

Решение. Вынесем общий множитель х за скобки:

х(5х-26)=0; каждый множитель может быть равным нулю:

х=0 или 5х-26=0 → 5х=26, делим обе части равенства на 5 и получаем: х=5,2.

Ответ: 0; 5,2.

Пример 3. 64x+4x 2 =0.

Решение. Вынесем общий множитель 4х за скобки:

4х(16+х)=0. У нас три множителя, 4≠0, следовательно, или х=0 или 16+х =0. Из последнего равенства получим х=-16.

Ответ: -16; 0.

Пример 4. (x-3) 2 +5x=9.

Решение. Применив формулу квадрата разности двух выражений раскроем скобки:

x 2 -6x+9+5x=9; преобразуем к виду: x 2 -6x+9+5x-9=0; приведем подобные слагаемые:

x 2 -x=0; вынесем х за скобки, получаем: x (x-1)=0. Отсюда или х=0 или х-1=0 → х=1.

Ответ: 0; 1.

III. ax 2 +c=0 – неполное квадратное уравнение (b=0 ); Решение: ax 2 =-c → x 2 =-c/a.

Если (-c/a)<0 , то действительных корней нет. Если (-с/а)>0

Пример 5. x 2 -49=0.

Решение.

x 2 =49, отсюда x=±7. Ответ: -7; 7.

Пример 6. 9x 2 -4=0.

Решение.

Часто требуется найти сумму квадратов (x 1 2 +x 2 2) или сумму кубов (x 1 3 +x 2 3) корней квадратного уравнения, реже — сумму обратных значений квадратов корней или сумму арифметических квадратных корней из корней квадратного уравнения:

Помочь в этом может теорема Виета:

x 2 +px+q=0

x 1 +x 2 =-p; x 1 ∙x 2 =q.

Выразим через p и q :

1) сумму квадратов корней уравнения x 2 +px+q=0;

2) сумму кубов корней уравнения x 2 +px+q=0.

Решение.

1) Выражение x 1 2 +x 2 2 получится, если взвести в квадрат обе части равенства x 1 +x 2 =-p;

(x 1 +x 2) 2 =(-p) 2 ; раскрываем скобки: x 1 2 +2x 1 x 2 + x 2 2 =p 2 ; выражаем искомую сумму: x 1 2 +x 2 2 =p 2 -2x 1 x 2 =p 2 -2q. Мы получили полезное равенство: x 1 2 +x 2 2 =p 2 -2q.

2) Выражение x 1 3 +x 2 3 представим по формуле суммы кубов в виде:

(x 1 3 +x 2 3)=(x 1 +x 2)(x 1 2 -x 1 x 2 +x 2 2)=-p·(p 2 -2q-q)=-p·(p 2 -3q).

Еще одно полезное равенство: x 1 3 +x 2 3 =-p·(p 2 -3q).

Примеры.

3) x 2 -3x-4=0. Не решая уравнение, вычислите значение выражения x 1 2 +x 2 2 .

Решение.

x 1 +x 2 =-p=3, а произведение x 1 ∙x 2 =q= в примере 1 ) равенство:

x 1 2 +x 2 2 =p 2 -2q. У нас -p =x 1 +x 2 =3 → p 2 =3 2 =9; q= x 1 x 2 =-4. Тогда x 1 2 +x 2 2 =9-2·(-4)=9+8=17.

Ответ: x 1 2 +x 2 2 =17.

4) x 2 -2x-4=0. Вычислить: x 1 3 +x 2 3 .

Решение.

По теореме Виета сумма корней этого приведенного квадратного уравнения x 1 +x 2 =-p=2, а произведение x 1 ∙x 2 =q= -4. Применим полученное нами (в примере 2 ) равенство: x 1 3 +x 2 3 =-p·(p 2 -3q)= 2·(2 2 -3·(-4))=2·(4+12)=2·16=32.

Ответ: x 1 3 +x 2 3 =32.

Вопрос: а если нам дано не приведенное квадратное уравнение? Ответ: его всегда можно «привести», разделив почленно на первый коэффициент.

5) 2x 2 -5x-7=0. Не решая, вычислить: x 1 2 +x 2 2 .

Решение. Нам дано полное квадратное уравнение. Разделим обе части равенства на 2 (первый коэффициент) и получим приведенное квадратное уравнение: x 2 -2,5x-3,5=0.

По теореме Виета сумма корней равна 2,5 ; произведение корней равно -3,5 .

Решаем так же, как пример 3) , используя равенство: x 1 2 +x 2 2 =p 2 -2q.

x 1 2 +x 2 2 =p 2 -2q= 2,5 2 -2∙(-3,5)=6,25+7=13,25.

Ответ: x 1 2 +x 2 2 =13,25.

6) x 2 -5x-2=0. Найти:

Преобразуем это равенство и, заменив по теореме Виета сумму корней через -p , а произведение корней через q , получим еще одну полезную формулу. При выводе формулы использовали равенство 1): x 1 2 +x 2 2 =p 2 -2q.

В нашем примере x 1 +x 2 =-p=5; x 1 ∙x 2 =q= -2. Подставляем эти значения в полученную формулу:

7) x 2 -13x+36=0. Найти:

Преобразуем эту сумму и получим формулу, по которой можно будет находить сумму арифметических квадратных корней из корней квадратного уравнения.

У нас x 1 +x 2 =-p=13; x 1 ∙x 2 =q=36 . Подставляем эти значения в выведенную формулу:

Совет : всегда проверяйте возможность нахождения корней квадратного уравнения по подходящему способу, ведь 4 рассмотренные полезные формулы позволяют быстро выполнить задание, прежде всего, в тех случаях, когда дискриминант — «неудобное» число. Во всех простых случаях находите корни и оперируйте ими. Например, в последнем примере подберем корни по теореме Виета: сумма корней должна быть равна 13 , а произведение корней 36 . Что это за числа? Конечно, 4 и 9. А теперь считайте сумму квадратных корней из этих чисел: 2+3=5. Вот так то!

I. Теорема Виета для приведенного квадратного уравнения.

Сумма корней приведенного квадратного уравнения x 2 +px+q=0 равна второму коэффициенту, взятому с противоположным знаком, а произведение корней равно свободному члену:

x 1 +x 2 =-p; x 1 ∙x 2 =q.

Найти корни приведенного квадратного уравнения, используя теорему Виета.

Пример 1) x 2 -x-30=0. Это приведенное квадратное уравнение ( x 2 +px+q=0) , второй коэффициент p=-1 , а свободный член q=-30. Сначала убедимся, что данное уравнение имеет корни, и что корни (если они есть) будут выражаться целыми числами. Для этого достаточно, чтобы дискриминант был полным квадратом целого числа.

Находим дискриминант D =b 2 — 4ac=(-1) 2 -4∙1∙(-30)=1+120=121=11 2 .

Теперь по теореме Виета сумма корней должна быть равна второму коэффициенту, взятому с противоположным знаком, т.е. (-p ), а произведение равно свободному члену, т.е. (q ). Тогда:

x 1 +x 2 =1; x 1 ∙x 2 =-30. Нам надо подобрать такие два числа, чтобы их произведение было равно -30 , а сумма – единице . Это числа -5 и 6 . Ответ: -5; 6.

Пример 2) x 2 +6x+8=0. Имеем приведенное квадратное уравнение со вторым коэффициентом р=6 и свободным членом q=8 . Убедимся, что есть целочисленные корни. Найдем дискриминант D 1 D 1 =3 2 -1∙8=9-8=1=1 2 . Дискриминант D 1 является полным квадратом числа 1 , значит, корни данного уравнения являются целыми числами. Подберем корни по теореме Виета: сумма корней равна –р=-6 , а произведение корней равно q=8 . Это числа -4 и -2 .

На самом деле: -4-2=-6=-р; -4∙(-2)=8=q. Ответ: -4; -2.

Пример 3) x 2 +2x-4=0 . В этом приведенном квадратном уравнении второй коэффициент р=2 , а свободный член q=-4 . Найдем дискриминант D 1 , так как второй коэффициент – четное число. D 1 =1 2 -1∙(-4)=1+4=5. Дискриминант не является полным квадратом числа, поэтому, делаем вывод : корни данного уравнения не являются целыми числами и найти их по теореме Виета нельзя. Значит, решим данное уравнение, как обычно, по формулам (в данном случае по формулам ). Получаем:

Пример 4). Составьте квадратное уравнение по его корням, если x 1 =-7, x 2 =4.

Решение. Искомое уравнение запишется в виде: x 2 +px+q=0 , причем, на основании теоремы Виета –p=x 1 +x 2 =-7+4=-3 → p=3; q=x 1 ∙x 2 =-7∙4=-28 . Тогда уравнение примет вид: x 2 +3x-28=0.

Пример 5). Составьте квадратное уравнение по его корням, если:

II. Теорема Виета для полного квадратного уравнения ax 2 +bx+c=0.

Сумма корней равна минус b , деленному на а , произведение корней равно с , деленному на а:

x 1 +x 2 =-b/a; x 1 ∙x 2 =c/a.

Пример 6). Найти сумму корней квадратного уравнения 2x 2 -7x-11=0 .

Решение.

Убеждаемся, что данное уравнение будет иметь корни. Для этого достаточно составить выражение для дискриминанта, и, не вычисляя его, просто убедиться, что дискриминант больше нуля. D =7 2 -4∙2∙(-11)>0 . А теперь воспользуемся теоремой Виета для полных квадратных уравнений.

x 1 +x 2 =-b:a =- (-7):2=3,5.

Пример 7) . Найдите произведение корней квадратного уравнения 3x 2 +8x-21=0.

Решение.

Найдем дискриминант D 1 , так как второй коэффициент (8 ) является четным числом. D 1 =4 2 -3∙(-21)=16+63=79>0 . Квадратное уравнение имеет 2 корня, по теореме Виета произведение корней x 1 ∙x 2 =c:a =-21:3=-7.

I. ax 2 +bx+c=0 – квадратное уравнение общего вида

Дискриминант D=b 2 - 4ac.

Если D>0 , то имеем два действительных корня:

Если D=0 , то имеем единственный корень (или два равных корня) х=-b/(2a) .

Если D<0, то действительных корней нет.

Пример 1) 2x 2 +5x-3=0.

Решение. a =2; b =5; c =-3.

D=b 2 — 4ac =5 2 -4∙2∙(-3)=25+24=49=7 2 >0; 2 действительных корня.

4x 2 +21x+5=0.

Решение. a =4; b =21; c =5.

D=b 2 — 4ac =21 2 — 4∙4∙5=441-80=361=19 2 >0; 2 действительных корня.

II. ax 2 +bx+c=0 – квадратное уравнение частного вида при четном втором

коэффициенте b

Пример 3) 3x 2 -10x+3=0.

Решение. a =3; b =-10 (четное число ); c =3.

Пример 4) 5x 2 -14x-3=0.

Решение. a =5; b = -14 (четное число ); c =-3.

Пример 5) 71x 2 +144x+4=0.

Решение. a =71; b =144 (четное число ); c =4.

Пример 6) 9x 2 -30x+25=0.

Решение. a =9; b =-30 (четное число ); c =25.

III. ax 2 +bx+c=0 – квадратное уравнение частного вида при условии : a-b+c=0.

Первый корень всегда равен минус единице, а второй корень равен минус с , деленному на а :

x 1 =-1, x 2 =-c/a.

Пример 7) 2x 2 +9x+7=0.

Решение. a =2; b =9; c =7. Проверим равенство: a-b+c=0. Получаем: 2-9+7=0 .

Тогда x 1 =-1, x 2 =-c/a=-7/2=-3,5. Ответ: -1; -3,5.

IV. ax 2 +bx+c=0 – квадратное уравнение частного вида при условии: a+b+c=0.

Первый корень всегда равен единице, а второй корень равен с , деленному на а :

x 1 =1, x 2 =c/a .

Пример 8) 2x 2 -9x+7=0.

Решение. a =2; b =-9; c =7. Проверим равенство: a+b+c=0. Получаем: 2-9+7=0 .

Тогда x 1 =1, x 2 =c/a=7/2=3,5. Ответ: 1; 3,5.

Страница 1 из 1 1

В этом видео мы разберём целый комплект линейных уравнений, которые решаются по одному и тому же алгоритму — потому и они и называются простейшими.

Для начала определимся: что такое линейное уравнение и какое их них называть простейшим?

Линейное уравнение — такое, в котором присутствует лишь одна переменная, причём исключительно в первой степени.

Под простейшим уравнением подразумевается конструкция:

Все остальные линейные уравнения сводятся к простейшим с помощью алгоритма:

1. Раскрыть скобки, если они есть;
2. Перенести слагаемые, содержащие переменную, в одну сторону от знака равенства, а слагаемые без переменной — в другую;
3. Привести подобные слагаемые слева и справа от знака равенства;
4. Разделить полученное уравнение на коэффициент при переменной $x$ .

Разумеется, этот алгоритм помогает не всегда. Дело в том, что иногда после всех этих махинаций коэффициент при переменной $x$ оказывается равен нулю. В этом случае возможны два варианта:

1. Уравнение вообще не имеет решений. Например, когда получается что-нибудь в духе $0\cdot x=8$, т.е. слева стоит ноль, а справа — число, отличное от нуля. В видео ниже мы рассмотрим сразу несколько причин, по которым возможна такая ситуация.
2. Решение — все числа. Единственный случай, когда такое возможно — уравнение свелось к конструкции $0\cdot x=0$. Вполне логично, что какой бы $x$ мы ни подставили, все равно получится «ноль равен нулю», т.е. верное числовое равенство.

А теперь давайте посмотрим, как всё это работает на примере реальных задач.

Примеры решения уравнений

Сегодня мы занимаемся линейными уравнениями, причем только простейшими. Вообще, под линейным уравнением подразумевается всякое равенство, содержащее в себе ровно одну переменную, и она идет лишь в первой степени.

Решаются такие конструкции примерно одинаково:

1. Прежде всего необходимо раскрыть скобки, если они есть (как в нашем последнем примере);
2. Затем свести подобные
3. Наконец, уединить переменную, т.е. всё, что связано с переменной — слагаемые, в которых она содержится — перенести в одну сторону, а всё, что останется без неё, перенести в другую сторону.

Затем, как правило, нужно привести подобные с каждой стороны полученного равенства, а после этого останется лишь разделить на коэффициент при «иксе», и мы получим окончательный ответ.

В теории это выглядит красиво и просто, однако на практике даже опытные ученики старших классов могут допускать обидные ошибки в достаточно простых линейных уравнениях. Обычно ошибки допускаются либо при раскрытии скобок, либо при подсчёте «плюсов» и «минусов».

Кроме того, бывает так, что линейное уравнение вообще не имеет решений, или так, что решением является вся числовая прямая, т.е. любое число. Эти тонкости мы и разберем в сегодняшнем уроке. Но начнем мы, как вы уже поняли, с самых простых задач.

Схема решения простейших линейных уравнений

Для начала давайте я еще раз напишу всю схему решения простейших линейных уравнений:

1. Раскрываем скобки, если они есть.
2. Уединяем переменные, т.е. все, что содержит «иксы» переносим в одну сторону, а без «иксов» — в другую.
3. Приводим подобные слагаемые.
4. Разделяем все на коэффициент при «иксе».

Разумеется, эта схема работает не всегда, в ней есть определенные тонкости и хитрости, и сейчас мы с ними и познакомимся.

Решаем реальные примеры простых линейных уравнений

Задача №1

На первом шаге от нас требуется раскрыть скобки. Но их в этом примере нет, поэтому пропускаем данный этап. На втором шаге нам нужно уединить переменные. Обратите внимание: речь идет лишь об отдельных слагаемых. Давайте запишем:

Приводим подобные слагаемые слева и справа, но тут уже это сделано. Поэтому переходим к четвертому шагу: разделить на коэффициент:

\[\frac{6x}{6}=-\frac{72}{6}\]

Вот мы и получили ответ.

Задача №2

В этой задаче мы можем наблюдать скобки, поэтому давайте раскроем их:

И слева и справа мы видим примерно одну и ту же конструкцию, но давайте действовать по алгоритму, т.е. уединяем переменные:

Приведем подобные:

При каких корнях это выполняется. Ответ: при любых. Следовательно, можно записать, что $x$ — любое число.

Задача №3

Третье линейное уравнение уже интересней:

\[\left(6-x \right)+\left(12+x \right)-\left(3-2x \right)=15\]

Тут есть несколько скобок, однако они ни на что не умножаются, просто перед ними стоят различные знаки. Давайте раскроем их:

Выполняем второй уже известный нам шаг:

\[-x+x+2x=15-6-12+3\]

Посчитаем:

Выполняем последний шаг — делим все на коэффициент при «икс»:

\[\frac{2x}{x}=\frac{0}{2}\]

Что необходимо помнить при решении линейных уравнений

Если отвлечься от слишком простых задач, то я бы хотел сказать следующее:

• Как я говорил выше, далеко не каждое линейное уравнение имеет решение — иногда корней просто нет;
• Даже если корни есть, среди них может затесаться ноль — ничего страшного в этом нет.

Ноль — такое же число, как и остальные, не стоит его как-то дискриминировать или считать, что если у вас получился ноль, то вы что-то сделали неправильно.

Еще одна особенность связана с раскрытием скобок. Обратите внимание: когда перед ними стоит «минус», то мы его убираем, однако в скобках знаки меняем на противоположные . А дальше мы можем раскрывать ее по стандартным алгоритмам: мы получим то, что видели в выкладках выше.

Понимание этого простого факта позволит вам не допускать глупые и обидные ошибки в старших классах, когда выполнение подобных действий считается самим собой разумеющимся.

Решение сложных линейных уравнений

Перейдем к более сложным уравнениям. Теперь конструкции станут сложнее и при выполнении различных преобразований возникнет квадратичная функция. Однако не стоит этого бояться, потому что если по замыслу автора мы решаем линейное уравнение, то в процессе преобразования все одночлены, содержащие квадратичную функцию, обязательно сократятся.

Пример №1

Очевидно, что первым делом нужно раскрыть скобки. Давайте это сделаем очень аккуратно:

Теперь займемся уединением:

\[-x+6{{x}^{2}}-6{{x}^{2}}+x=-12\]

Приводим подобные:

Очевидно, что у данного уравнения решений нет, поэтому в ответе так и запишем:

\[\varnothing \]

или корней нет.

Пример №2

Выполняем те же действия. Первый шаг:

Перенесем все, что с переменной, влево, а без нее — вправо:

Приводим подобные:

Очевидно, что данное линейное уравнение не имеет решения, поэтому так и запишем:

\[\varnothing \],

либо корней нет.

Нюансы решения

Оба уравнения полностью решены. На примере этих двух выражений мы ещё раз убедились, что даже в самых простых линейных уравнениях всё может быть не так просто: корней может быть либо один, либо ни одного, либо бесконечно много. В нашем случае мы рассмотрели два уравнения, в обоих корней просто нет.

Но я бы хотел обратить ваше внимание на другой факт: как работать со скобками и как их раскрывать, если перед ними стоит знак «минус». Рассмотрим вот это выражение:

Прежде чем раскрывать, нужно перемножить всё на «икс». Обратите внимание: умножается каждое отдельное слагаемое . Внутри стоит два слагаемых — соответственно, два слагаемых и умножается.

И только после того, когда эти, казалось бы, элементарные, но очень важные и опасные преобразования выполнены, можно раскрывать скобку с точки зрения того, что после неё стоит знак «минус». Да, да: только сейчас, когда преобразования выполнены, мы вспоминаем, что перед скобками стоит знак «минус», а это значит, что все, что в низ, просто меняет знаки. При этом сами скобки исчезают и, что самое главное, передний «минус» тоже исчезает.

Точно также мы поступаем и со вторым уравнением:

Я не случайно обращаю внимание на эти мелкие, казалось бы, незначительные факты. Потому что решение уравнений — это всегда последовательность элементарных преобразований, где неумение чётко и грамотно выполнять простые действия приводит к тому, что ученики старших классов приходят ко мне и вновь учатся решать вот такие простейшие уравнения.

Разумеется, придёт день, и вы отточите эти навыки до автоматизма. Вам уже не придётся каждый раз выполнять столько преобразований, вы всё будете писать в одну строчку. Но пока вы только учитесь, нужно писать каждое действие отдельно.

Решение ещё более сложных линейных уравнений

То, что мы сейчас будем решать, уже сложно назвать простейшими задача, однако смысл остается тем же самым.

Задача №1

\[\left(7x+1 \right)\left(3x-1 \right)-21{{x}^{2}}=3\]

Давайте перемножим все элементы в первой части:

Давайте выполним уединение:

Приводим подобные:

Выполняем последний шаг:

\[\frac{-4x}{4}=\frac{4}{-4}\]

Вот наш окончательный ответ. И, несмотря на то, что у нас в процессе решения возникали коэффициенты с квадратичной функцией, однако они взаимно уничтожились, что делает уравнение именно линейным, а не квадратным.

Задача №2

\[\left(1-4x \right)\left(1-3x \right)=6x\left(2x-1 \right)\]

Давайте аккуратно выполним первый шаг: умножаем каждый элемент из первой скобки на каждый элемент из второй. Всего должно получиться четыре новых слагаемых после преобразований:

А теперь аккуратно выполним умножение в каждом слагаемом:

Перенесем слагаемые с «иксом» влево, а без — вправо:

\[-3x-4x+12{{x}^{2}}-12{{x}^{2}}+6x=-1\]

Приводим подобные слагаемые:

Мы вновь получили окончательный ответ.

Нюансы решения

Важнейшее замечание по поводу этих двух уравнений состоит в следующем: как только мы начинаем умножать скобки, в которых находится более чем оно слагаемое, то выполняется это по следующему правилу: мы берем первое слагаемое из первой и перемножаем с каждым элементом со второй; затем берем второй элемент из первой и аналогично перемножаем с каждым элементом со второй. В итоге у нас получится четыре слагаемых.

Об алгебраической сумме

На последнем примере я хотел бы напомнить ученикам, что такое алгебраическая сумма. В классической математике под $1-7$ мы подразумеваем простую конструкцию: из единицы вычитаем семь. В алгебре же мы подразумеваем под этим следующее: к числу «единица» мы прибавляем другое число, а именно «минус семь». Этим алгебраическая сумма отличается от обычной арифметической.

Как только при выполнении всех преобразований, каждого сложения и умножения вы начнёте видеть конструкции, аналогичные вышеописанным, никаких проблем в алгебре при работе с многочленами и уравнениями у вас просто не будет.

В заключение давайте рассмотрим ещё пару примеров, которые будут ещё более сложными, чем те, которые мы только что рассмотрели, и для их решения нам придётся несколько расширить наш стандартный алгоритм.

Решение уравнений с дробью

Для решения подобных заданий к нашему алгоритму придется добавить еще один шаг. Но для начала я напомню наш алгоритм:

1. Раскрыть скобки.
2. Уединить переменные.
3. Привести подобные.
4. Разделить на коэффициент.

Увы, этот прекрасный алгоритм при всей его эффективности оказывается не вполне уместным, когда перед нами дроби. А в том, что мы увидим ниже, у нас и слева, и справа в обоих уравнениях есть дробь.

Как работать в этом случае? Да всё очень просто! Для этого в алгоритм нужно добавить ещё один шаг, который можно совершить как перед первым действием, так и после него, а именно избавиться от дробей. Таким образом, алгоритм будет следующим:

1. Избавиться от дробей.
2. Раскрыть скобки.
3. Уединить переменные.
4. Привести подобные.
5. Разделить на коэффициент.

Что значит «избавиться от дробей»? И почему выполнять это можно как после, так и перед первым стандартным шагом? На самом деле в нашем случае все дроби являются числовыми по знаменателю, т.е. везде в знаменателе стоит просто число. Следовательно, если мы обе части уравнения домножим на это число, то мы избавимся от дробей.

Пример №1

\[\frac{\left(2x+1 \right)\left(2x-3 \right)}{4}={{x}^{2}}-1\]

Давайте избавимся от дробей в этом уравнении:

\[\frac{\left(2x+1 \right)\left(2x-3 \right)\cdot 4}{4}=\left({{x}^{2}}-1 \right)\cdot 4\]

Обратите внимание: на «четыре» умножается все один раз, т.е. если у вас две скобки, это не значит, что каждую из них нужно умножать на «четыре». Запишем:

\[\left(2x+1 \right)\left(2x-3 \right)=\left({{x}^{2}}-1 \right)\cdot 4\]

Теперь раскроем:

Выполняем уединение переменной:

Выполняем приведение подобных слагаемых:

\[-4x=-1\left| :\left(-4 \right) \right.\]

\[\frac{-4x}{-4}=\frac{-1}{-4}\]

Мы получили окончательное решение, переходим ко второму уравнению.

Пример №2

\[\frac{\left(1-x \right)\left(1+5x \right)}{5}+{{x}^{2}}=1\]

Здесь выполняем все те же действия:

\[\frac{\left(1-x \right)\left(1+5x \right)\cdot 5}{5}+{{x}^{2}}\cdot 5=5\]

\[\frac{4x}{4}=\frac{4}{4}\]

Задача решена.

Вот, собственно, и всё, что я хотел сегодня рассказать.

Ключевые моменты

Ключевые выводы следующие:

• Знать алгоритм решения линейных уравнений.
• Умение раскрывать скобки.
• Не стоит переживать, если где-то у вас появляются квадратичные функции, скорее всего, в процессе дальнейших преобразований они сократятся.
• Корни в линейных уравнениях, даже самых простых, бывают трех типов: один единственный корень, вся числовая прямая является корнем, корней нет вообще.

Надеюсь, этот урок поможет вам освоить несложную, но очень важную для дальнейшего понимания всей математики тему. Если что-то непонятно, заходите на сайт, решайте примеры, представленные там. Оставайтесь с нами, вас ждет еще много интересного!

На этапе подготовки к заключительному тестированию учащимся старших классов необходимо подтянуть знания по теме «Показательные уравнения». Опыт прошлых лет свидетельствует о том, что подобные задания вызывают у школьников определенные затруднения. Поэтому старшеклассникам, независимо от уровня их подготовки, необходимо тщательно усвоить теорию, запомнить формулы и понять принцип решения таких уравнений. Научившись справляться с данным видом задач, выпускники смогут рассчитывать на высокие баллы при сдаче ЕГЭ по математике.

Готовьтесь к экзаменационному тестированию вместе со «Школково»!

При повторении пройденных материалов многие учащиеся сталкиваются с проблемой поиска нужных для решения уравнений формул. Школьный учебник не всегда находится под рукой, а отбор необходимой информации по теме в Интернете занимает долгое время.

Образовательный портал «Школково» предлагает ученикам воспользоваться нашей базой знаний. Мы реализуем совершенно новый метод подготовки к итоговому тестированию. Занимаясь на нашем сайте, вы сможете выявить пробелы в знаниях и уделить внимание именно тем заданиям, которые вызывают наибольшие затруднения.

Преподаватели «Школково» собрали, систематизировали и изложили весь необходимый для успешной сдачи ЕГЭ материал в максимально простой и доступной форме.

Основные определения и формулы представлены в разделе «Теоретическая справка».

Для лучшего усвоения материала рекомендуем попрактиковаться в выполнении заданий. Внимательно просмотрите представленные на данной странице примеры показательных уравнений с решением, чтобы понять алгоритм вычисления. После этого приступайте к выполнению задач в разделе «Каталоги». Вы можете начать с самых легких заданий или сразу перейти к решению сложных показательных уравнений с несколькими неизвестными или . База упражнений на нашем сайте постоянно дополняется и обновляется.

Те примеры с показателями, которые вызвали у вас затруднения, можно добавить в «Избранное». Так вы можете быстро найти их и обсудить решение с преподавателем.

Чтобы успешно сдать ЕГЭ, занимайтесь на портале «Школково» каждый день!