Наиболее просто устроены матрицы диагонального вида . Возникает вопрос, нельзя ли найти базис, в котором матрица линейного оператора имела бы диагональный вид. Такой базис существует.
Пусть дано линейное пространство R n и действующий в нем линейный оператор A; в этом случае оператор A переводит R n в себя, то есть A:R n → R n .

Определение. Ненулевой вектор x называется собственным вектором оператора A , если оператор A переводит x в коллинеарный ему вектор, то есть . Число λ называется собственным значением или собственным числом оператора A, соответствующим собственному вектору x .
Отметим некоторые свойства собственных чисел и собственных векторов.
1. Любая линейная комбинация собственных векторов оператора A, отвечающих одному и тому же собственному числу λ, является собственным вектором с тем же собственным числом.
2. Собственные векторы оператора A с попарно различными собственными числами λ 1 , λ 2 , …, λ m линейно независимы.
3. Если собственные числа λ 1 =λ 2 = λ m = λ, то собственному числу λ соответствует не более m линейно независимых собственных векторов.

Итак, если имеется n линейно независимых собственных векторов , соответствующих различным собственным числам λ 1 , λ 2 , …, λ n , то они линейно независимы, следовательно, их можно принять за базис пространства R n . Найдем вид матрицы линейного оператора A в базисе из его собственных векторов, для чего подействуем оператором A на базисные векторы: тогда .
Таким образом, матрица линейного оператора A в базисе из его собственных векторов имеет диагональный вид, причем по диагонали стоят собственные числа оператора A.
Существует ли другой базис, в котором матрица имеет диагональный вид? Ответ на поставленный вопрос дает следующая теорема.

Теорема. Матрица линейного оператора A в базисе (i = 1..n) имеет диагональный вид тогда и только тогда, когда все векторы базиса - собственные векторы оператора A.

Правило отыскания собственных чисел и собственных векторов

Пусть дан вектор , где x 1 , x 2 , …, x n - координаты вектора x относительно базиса и x - собственный вектор линейного оператора A, соответствующий собственному числу λ , то есть . Это соотношение можно записать в матричной форме

. (*)

Уравнение (*) можно рассматривать как уравнение для отыскания x , причем , то есть нас интересуют нетривиальные решения, поскольку собственный вектор не может быть нулевым. Известно, что нетривиальные решения однородной системы линейных уравнений существуют тогда и только тогда, когда det(A - λE) = 0. Таким образом, для того, чтобы λ было собственным числом оператора A необходимо и достаточно, чтобы det(A - λE) = 0.
Если уравнение (*) расписать подробно в координатной форме, то получим систему линейных однородных уравнений:

(1)
где - матрица линейного оператора.

Система (1) имеет ненулевое решение, если ее определитель D равен нулю

Получили уравнение для нахождения собственных чисел.
Это уравнение называется характеристическим уравнением, а его левая часть - характеристическим многочленом матрицы (оператора) A. Если характеристический многочлен не имеет вещественных корней, то матрица A не имеет собственных векторов и ее нельзя привести к диагональному виду.
Пусть λ 1 , λ 2 , …, λ n - вещественные корни характеристического уравнения, причем среди них могут быть и кратные. Подставляя по очереди эти значения в систему (1), находим собственные векторы.

Пример 12. Линейный оператор A действует в R 3 по закону , где x 1 , x 2 , .., x n - координаты вектора в базисе , , . Найти собственные числа и собственные векторы этого оператора.
Решение. Строим матрицу этого оператора:
.
Составляем систему для определения координат собственных векторов:

Составляем характеристическое уравнение и решаем его:

.
λ 1,2 = -1, λ 3 = 3.
Подставляя λ = -1 в систему, имеем:
или
Так как , то зависимых переменных два, а свободное одно.
Пусть x 1 - свободное неизвестное, тогда Решаем эту систему любым способом и находим общее решение этой системы: Фундаментальная система решений состоит из одного решения, так как n - r = 3 - 2 = 1.
Множество собственных векторов, отвечающих собственному числу λ = -1, имеет вид: , где x 1 - любое число, отличное от нуля. Выберем из этого множества один вектор, например, положив x 1 = 1: .
Рассуждая аналогично, находим собственный вектор, отвечающий собственному числу λ = 3: .
В пространстве R 3 базис состоит из трех линейно независимых векторов, мы же получили только два линейно независимых собственных вектора, из которых базис в R 3 составить нельзя. Следовательно, матрицу A линейного оператора привести к диагональному виду не можем.

Пример 13. Дана матрица .
1. Доказать, что вектор является собственным вектором матрицы A. Найти собственное число, соответствующее этому собственному вектору.
2. Найти базис, в котором матрица A имеет диагональный вид.
Решение.
1. Если , то x - собственный вектор

.
Вектор (1, 8, -1) - собственный вектор. Собственное число λ = -1.
Диагональный вид матрица имеет в базисе, состоящем из собственных векторов. Один из них известен. Найдем остальные.
Собственные векторы ищем из системы:

Характеристическое уравнение: ;
(3 + λ)[-2(2-λ)(2+λ)+3] = 0; (3+λ)(λ 2 - 1) = 0
λ 1 = -3, λ 2 = 1, λ 3 = -1.
Найдем собственный вектор, отвечающий собственному числу λ = -3:

Ранг матрицы этой системы равен двум и равен числу неизвестных, поэтому эта система имеет только нулевое решение x 1 = x 3 = 0. x 2 здесь может быть любым, отличным от нуля, например, x 2 = 1. Таким образом, вектор (0,1,0) является собственным вектором, отвечающим λ = -3. Проверим:
.
Если λ = 1, то получаем систему
Ранг матрицы равен двум. Последнее уравнение вычеркиваем.
Пусть x 3 - свободное неизвестное. Тогда x 1 = -3x 3 , 4x 2 = 10x 1 - 6x 3 = -30x 3 - 6x 3 , x 2 = -9x 3 .
Полагая x 3 = 1, имеем (-3,-9,1) - собственный вектор, отвечающий собственному числу λ = 1. Проверка:

.
Так как собственные числа действительные и различны, то векторы, им отвечающие, линейно независимы, поэтому их можно принять за базис в R 3 . Таким образом, в базисе , , матрица A имеет вид:
.
Не всякую матрицу линейного оператора A:R n → R n можно привести к диагональному виду, поскольку для некоторых линейных операторов линейно независимых собственных векторов может быть меньше n. Однако, если матрица симметрическая, то корню характеристического уравнения кратности m соответствует ровно m линейно независимых векторов.

Определение. Симметрической матрицей называется квадратная матрица, в которой элементы, симметричные относительно главной диагонали, равны, то есть в которой .
Замечания. 1. Все собственные числа симметрической матрицы вещественны.
2. Собственные векторы симметрической матрицы, соответствующие попарно различным собственным числам, ортогональны.
В качестве одного из многочисленных приложений изученного аппарата, рассмотрим задачу об определении вида кривой второго порядка.

Собственные значения (числа) и собственные векторы.
Примеры решений

Будь собой

Из обоих уравнений следует, что .

Положим , тогда: .

В результате: – второй собственный вектор.

Повторим важные моменты решения:

– полученная система непременно имеет общее решение (уравнения линейно зависимы);

– «игрек» подбираем таким образом, чтобы он был целым и первая «иксовая» координата – целой, положительной и как можно меньше.

– проверяем, что частное решение удовлетворяет каждому уравнению системы.

Ответ .

Промежуточных «контрольных точек» было вполне достаточно, поэтому проверка равенств , в принципе, дело излишнее.

В различных источниках информации координаты собственных векторов довольно часто записывают не в столбцы, а в строки, например: (и, если честно, я сам привык записывать их строками) . Такой вариант приемлем, но в свете темы линейных преобразований технически удобнее использовать векторы-столбцы .

Возможно, решение показалась вам очень длинным, но это только потому, что я очень подробно прокомментировал первый пример.

Пример 2

Матрицы

Тренируемся самостоятельно! Примерный образец чистового оформления задачи в конце урока.

Иногда требуется выполнить дополнительное задание, а именно:

записать каноническое разложение матрицы

Что это такое?

Если собственные векторы матрицы образуют базис , то она представима в виде:

Где – матрица составленная из координат собственных векторов, – диагональная матрица с соответствующими собственными числами.

Такое разложение матрицы называют каноническим или диагональным .

Рассмотрим матрицу первого примера. Её собственные векторы линейно независимы (неколлинеарны)и образуют базис. Составим матрицу из их координат:

На главной диагонали матрицы в соответствующем порядке располагаются собственные числа, а остальные элементы равняются нулю:
– ещё раз подчёркиваю важность порядка: «двойка» соответствует 1-му вектору и посему располагается в 1-м столбце, «тройка» – 2-му вектору.

По обычному алгоритму нахождения обратной матрицы либо методом Гаусса-Жордана находим . Нет, это не опечатка! – перед вами редкое, как солнечное затмение событие, когда обратная совпала с исходной матрицей.

Осталось записать каноническое разложение матрицы :

Систему можно решить с помощью элементарных преобразований и в следующих примерах мы прибегнем к данному методу. Но здесь гораздо быстрее срабатывает «школьный» способ. Из 3-го уравнения выразим: – подставим во второе уравнение:

Поскольку первая координата нулевая, то получаем систему , из каждого уравнения которой следует, что .

И снова обратите внимание на обязательное наличие линейной зависимости . Если получается только тривиальное решение , то либо неверно найдено собственное число, либо с ошибкой составлена / решена система.

Компактные координаты даёт значение

Собственный вектор:

И ещё раз – проверяем, что найденное решение удовлетворяет каждому уравнению системы . В последующих пунктах и в последующих задачах рекомендую принять данное пожелание за обязательное правило.

2) Для собственного значения по такому же принципу получаем следующую систему:

Из 2-го уравнения системы выразим: – подставим в третье уравнение:

Поскольку «зетовая» координата равна нулю, то получаем систему , из каждого уравнения которой следует линейная зависимость .

Пусть

Проверяем, что решение удовлетворяет каждому уравнению системы.

Таким образом, собственный вектор: .

3) И, наконец, собственному значению соответствует система:

Второе уравнение выглядит самым простым, поэтому из него выразим и подставим в 1-е и 3-е уравнение:

Всё хорошо – выявилась линейная зависимость , которую подставляем в выражение :

В результате «икс» и «игрек» оказались выражены через «зет»: . На практике не обязательно добиваться именно таких взаимосвязей, в некоторых случаях удобнее выразить и через либо и через . Или даже «паровозиком» – например, «икс» через «игрек», а «игрек» через «зет»

Положим , тогда:

Проверяем, что найденное решение удовлетворяет каждому уравнению системы и записываем третий собственный вектор

Ответ : собственные векторы:

Геометрически эти векторы задают три различных пространственных направления («туда-обратно») , по которым линейное преобразование переводит ненулевые векторы (собственные векторы) в коллинеарные им векторы.

Если бы по условию требовалось найти каноническое разложение , то здесь это возможно, т.к. различным собственным числам соответствуют разные линейно независимые собственные векторы. Составляем матрицу из их координат, диагональную матрицу из соответствующих собственных значений и находим обратную матрицу .

Если же по условию нужно записать матрицу линейного преобразования в базисе из собственных векторов , то ответ даём в виде . Разница есть, и разница существенная! Ибо оная матрица – есть матрица «дэ».

Задача с более простыми вычислениями для самостоятельного решения:

Пример 5

Найти собственные векторы линейного преобразования, заданного матрицей

При нахождении собственных чисел постарайтесь не доводить дело до многочлена 3-й степени. Кроме того, ваши решения систем могут отличаться от моих решений – здесь нет однозначности; и векторы, которые вы найдёте, могут отличаться от векторов образца с точностью до пропорциональности их соответствующих координат. Например, и . Эстетичнее представить ответ в виде , но ничего страшного, если остановитесь и на втором варианте. Однако всему есть разумные пределы, версия смотрится уже не очень хорошо.

Примерный чистовой образец оформления задания в конце урока.

Как решать задачу в случае кратных собственных чисел?

Общий алгоритм остаётся прежним, но здесь есть свои особенности, и некоторые участки решения целесообразно выдержать в более строгом академичном стиле:

Пример 6

Найти собственные числа и собственные векторы

Решение

Конечно же, оприходуем сказочный первый столбец:

И, после разложения квадратного трёхчлена на множители:

В результате получены собственные числа , два из которых кратны.

Найдем собственные векторы:

1) С одиноким солдатом разделаемся по «упрощённой» схеме:

Из последних двух уравнений четко просматривается равенство , которое, очевидно, следует подставить в 1-е уравнение системы:

Лучшей комбинации не найти:
Собственный вектор:

2-3) Теперь снимаем пару часовых. В данном случае может получиться либо два, либо один собственный вектор. Невзирая на кратность корней, подставим значение в определитель , который приносит нам следующую однородную систему линейных уравнений :

Собственные векторы – это в точности векторы
фундаментальной системы решений

Собственно, на протяжении всего урока мы только и занимались тем, что находили векторы фундаментальной системы. Просто до поры до времени данный термин особо не требовался. Кстати, те ловкие студенты, которые в маскхалатах проскочили тему однородных уравнений , будут вынуждены вкурить её сейчас.

Единственное действие состояло в удалении лишних строк. В результате получена матрица «один на три» с формальной «ступенькой» посередине.
– базисная переменная, – свободные переменные. Свободных переменных две, следовательно, векторов фундаментальной системы тоже два .

Выразим базисную переменную через свободные переменные: . Нулевой множитель перед «иксом» позволяет принимать ему совершенно любые значения (что хорошо видно и из системы уравнений).

В контексте данной задачи общее решение удобнее записать не в строку, а в столбец:

Паре соответствует собственный вектор:
Паре соответствует собственный вектор:

Примечание : искушенные читатели могут подобрать данные векторы и устно – просто анализируя систему , но тут нужны некоторые знания: переменных – три, ранг матрицы системы – единица, значит, фундаментальная система решений состоит из 3 – 1 = 2 векторов. Впрочем, найдённые векторы отлично просматриваются и без этих знаний чисто на интуитивном уровне. При этом даже «красивее» запишется третий вектор: . Однако предостерегаю, в другом примере простого подбора может и не оказаться, именно поэтому оговорка предназначена для опытных людей. Кроме того, а почему бы не взять в качестве третьего вектора, скажем, ? Ведь его координаты тоже удовлетворяют каждому уравнение системы, и векторы линейно независимы. Такой вариант, в принципе, годен, но «кривоват», поскольку «другой» вектор представляет собой линейную комбинацию векторов фундаментальной системы.

Ответ : собственные числа: , собственные векторы:

Аналогичный пример для самостоятельного решения:

Пример 7

Найти собственные числа и собственные векторы

Примерный образец чистового оформления в конце урока.

Следует отметить, что и в 6-м и в 7-м примере получается тройка линейно независимых собственных векторов, и поэтому исходная матрица представима в каноническом разложении . Но такая малина бывает далеко не во всех случаях:

Пример 8

Решение : составим и решим характеристическое уравнение:

Определитель раскроем по первому столбцу:

Дальнейшие упрощения проводим согласно рассмотренной методике, избегая многочлена 3-й степени:

– собственные значения.

Найдем собственные векторы:

1) С корнем затруднений не возникает:

Не удивляйтесь, помимо комплекта в ходу также переменные – разницы тут никакой.

Из 3-го уравнения выразим – подставим в 1-е и 2-е уравнения:

Из обоих уравнений следует:

Пусть , тогда:

2-3) Для кратных значений получаем систему .

Запишем матрицу системы и с помощью элементарных преобразований приведём её к ступенчатому виду:

". В первой части изложены положения, минимально необходимые для понимания хемометрики, а во второй части - факты, которые необходимо знать для более глубокого постижения методов многомерного анализа. Изложение иллюстрируется примерами, выполненными в рабочей книге Excel Matrix.xls , которая сопровождает этот документ.

Ссылки на примеры помещены в текст как объекты Excel. Эти примеры имеют абстрактный характер, они никак не привязаны к задачам аналитической химии. Реальные примеры использования матричной алгебры в хемометрике рассмотрены в других текстах, посвященных разнообразным хемометрическим приложениям.

Большинство измерений, проводимых в аналитической химии, являются не прямыми, а косвенными . Это означает, что в эксперименте вместо значения искомого аналита C (концентрации) получается другая величина x (сигнал), связанная, но не равная C, т.е. x (C) ≠ С. Как правило, вид зависимости x (C) не известен, однако, к счастью, в аналитической химии большинство измерений пропорциональны. Это означает, что при увеличении концентрации С в a раз, сигнал X увеличится на столько же., т.е. x (a C) = a x (C). Кроме того, сигналы еще и аддитивны, так что сигнал от пробы, в которой присутствуют два вещества с концентрациями C 1 и C 2 , будет равен сумме сигналов от каждого компонента, т.е. x (C 1 + C 2) = x (C 1)+ x (C 2). Пропорциональность и аддитивность вместе дают линейность . Можно привести много примеров, иллюстрирующих принцип линейности, но достаточно упомянуть два самых ярких примера - хроматографию и спектроскопию. Вторая особенность, присущая эксперименту в аналитической химии - это многоканальность . Современное аналитическое оборудование одновременно измеряет сигналы для многих каналов. Например, измеряется интенсивность пропускания света сразу для нескольких длин волн, т.е. спектр. Поэтому в эксперименте мы имеем дело со множеством сигналов x 1 , x 2 ,...., x n , характеризующих набор концентраций C 1 ,C 2 , ..., C m веществ, присутствующих в изучаемой системе.

Рис. 1 Спектры

Итак, аналитический эксперимент характеризуется линейностью и многомерностью. Поэтому удобно рассматривать экспериментальные данные как векторы и матрицы и манипулировать с ними, используя аппарат матричной алгебры. Плодотворность такого подхода иллюстрирует пример, показанный на , где представлены три спектра, снятые для 200 длин волн от 4000 до 4796 cm −1 . Первый (x 1) и второй (x 2) спектры получены для стандартных образцов, в которых концентрация двух веществ A и B, известны: в первом образце [A] = 0.5, [B] = 0.1, а во втором образце [A] = 0.2, [B] = 0.6. Что можно сказать о новом, неизвестном образце, спектр которого обозначен x 3 ?

Рассмотрим три экспериментальных спектра x 1 , x 2 и x 3 как три вектора размерности 200. Средствами линейной алгебры можно легко показать, что x 3 = 0.1 x 1 +0.3 x 2 , поэтому в третьем образце очевидно присутствуют только вещества A и B в концентрациях [A] = 0.5×0.1 + 0.2×0.3 = 0.11 и [B] = 0.1×0.1 + 0.6×0.3 = 0.19.

1. Базовые сведения

1.1 Матрицы

Матрицей называется прямоугольная таблица чисел, например

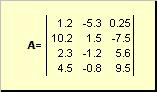
Рис. 2 Матрица

Матрицы обозначаются заглавными полужирными буквами (A ), а их элементы - соответствующими строчными буквами с индексами, т.е. a ij . Первый индекс нумерует строки, а второй - столбцы. В хемометрике принято обозначать максимальное значение индекса той же буквой, что и сам индекс, но заглавной. Поэтому матрицу A можно также записать как { a ij , i = 1,..., I ; j = 1,..., J }. Для приведенной в примере матрицы I = 4, J = 3 и a 23 = −7.5.

Пара чисел I и J называется размерностью матрицы и обознается как I ×J . Примером матрицы в хемометрике может служить набор спектров, полученный для I образцов на J длинах волн.

1.2. Простейшие операции с матрицами

Матрицы можно умножать на числа . При этом каждый элемент умножается на это число. Например -

Рис. 3 Умножение матрицы на число

Две матрицы одинаковой размерности можно поэлементно складывать и вычитать . Например,

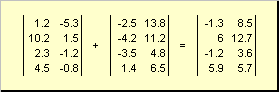
Рис. 4 Сложение матриц

В результате умножения на число и сложения получается матрица той же размерности.

Нулевой матрицей называется матрица, состоящая из нулей. Она обозначается O . Очевидно, что A +O = A , A −A = O и 0A = O .

Матрицу можно транспонировать . При этой операции матрица переворачивается, т.е. строки и столбцы меняются местами. Транспонирование обозначается штрихом, A " или индексом A t . Таким образом, если A = {a ij , i = 1,..., I ; j = 1,...,J }, то A t = {a ji , j = 1,...,J ; i = 1,..., I }. Например

Рис. 5 Транспонирование матрицы

Очевидно, что (A t) t = A , (A +B ) t = A t +B t .

1.3. Умножение матриц

Матрицы можно перемножать , но только в том случае, когда они имеют соответствующие размерности. Почему это так, будет ясно из определения. Произведением матрицы A , размерностью I ×K , и матрицы B , размерностью K ×J , называется матрица C , размерностью I ×J , элементами которой являются числа

Таким образом для произведения AB необходимо, чтобы число столбцов в левой матрице A было равно числу строк в правой матрице B . Пример произведения матриц -

Рис.6 Произведение матриц

Правило перемножения матриц можно сформулировать так. Для того, чтобы найти элемент матрицы C , стоящий на пересечении i -ой строки и j -ого столбца (c ij ) надо поэлементно перемножить i -ую строку первой матрицы A на j -ый столбец второй матрицы B и сложить все результаты. Так в показанном примере, элемент из третьей строки и второго столбца, получается как сумма поэлементных произведений третьей строки A и второго столбца B

Рис.7 Элемент произведения матриц

Произведение матриц зависит от порядка, т.е. AB ≠ BA , хотя бы по соображениям размерности. Говорят, что оно некоммутативно. Однако произведение матриц ассоциативно. Это означает, что ABC = (AB )C = A (BC ). Кроме того, оно еще и дистрибутивно, т.е. A (B +C ) = AB +AC . Очевидно, что AO = O .

1.4. Квадратные матрицы

Если число столбцов матрицы равно числу ее строк (I = J = N ), то такая матрица называется квадратной. В этом разделе мы будем рассматривать только такие матрицы. Среди этих матриц можно выделить матрицы, обладающие особыми свойствами.

Единичной матрицей (обозначается I, а иногда E ) называется матрица, у которой все элементы равны нулю, за исключением диагональных, которые равны 1, т.е.

Очевидно AI = IA = A .

Матрица называется диагональной , если все ее элементы, кроме диагональных (a ii ) равны нулю. Например

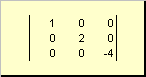
Рис. 8 Диагональная матрица

Матрица A называется верхней треугольной , если все ее элементы, лежащие ниже диагонали, равны нулю, т.е. a ij = 0, при i >j . Например

Рис. 9 Верхняя треугольная матрица

Аналогично определяется и нижняя треугольная матрица.

Матрица A называется симметричной , если A t = A . Иными словами a ij = a ji . Например

Рис. 10 Симметричная матрица

Матрица A называется ортогональной , если

A t A = AA t = I .

Матрица называется нормальной если

1.5. След и определитель

Следом квадратной матрицы A (обозначается Tr(A ) или Sp(A )) называется сумма ее диагональных элементов,

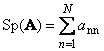
Например,

Рис. 11 След матрицы

Очевидно, что

Sp(α A ) = α Sp(A ) и

Sp(A +B ) = Sp(A )+ Sp(B ).

Можно показать, что

Sp(A ) = Sp(A t), Sp(I ) = N ,

а также, что

Sp(AB ) = Sp(BA ).

Другой важной характеристикой квадратной матрицы является ее определитель (обозначается det(A )). Определение определителя в общем случае довольно сложно, поэтому мы начнем с простейшего варианта - матрицы A размерностью (2×2). Тогда

Для матрицы (3×3) определитель будет равен

В случае матрицы (N ×N ) определитель вычисляется как сумма 1·2·3· ... ·N = N ! слагаемых, каждый из которых равен

Индексы k 1 , k 2 ,..., k N определяются как всевозможные упорядоченные перестановки r чисел в наборе (1, 2, ... , N ). Вычисление определителя матрицы - это сложная процедура, которую на практике осуществляется с помощью специальных программ. Например,

Рис. 12 Определитель матрицы

Отметим только очевидные свойства:

det(I ) = 1, det(A ) = det(A t),

det(AB ) = det(A )det(B ).

1.6. Векторы

Если матрица состоит только из одного столбца (J = 1), то такой объект называется вектором . Точнее говоря, вектором-столбцом. Например

Можно рассматривать и матрицы, состоящие из одной строки, например

Этот объект также является вектором, но вектором-строкой . При анализе данных важно понимать, с какими векторами мы имеем дело - со столбцами или строками. Так спектр, снятый для одного образца можно рассматривать как вектор-строку. Тогда набор спектральных интенсивностей на какой-то длине волны для всех образцов нужно трактовать как вектор-столбец.

Размерностью вектора называется число его элементов.

Ясно, что всякий вектор-столбец можно превратить в вектор-строку транспонированием, т.е.

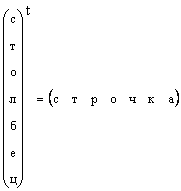
В тех случаях, когда форма вектора специально не оговаривается, а просто говорится вектор, то имеют в виду вектор-столбец. Мы тоже будем придерживаться этого правила. Вектор обозначается строчной прямой полужирной буквой. Нулевым вектором называется вектор, все элементы которого раны нулю. Он обозначается 0 .

1.7. Простейшие операции с векторами

Векторы можно складывать и умножать на числа так же, как это делается с матрицами. Например,

Рис. 13 Операции с векторами

Два вектора x и y называются колинеарными , если существует такое число α, что

1.8. Произведения векторов

Два вектора одинаковой размерности N можно перемножить. Пусть имеются два вектора x = (x 1 , x 2 ,...,x N) t и y = (y 1 , y 2 ,..., y N) t . Руководствуясь правилом перемножения "строка на столбец", мы можем составить из них два произведения: x t y и xy t . Первое произведение

называется скалярным или внутренним . Его результат - это число. Для него также используется обозначение (x ,y )= x t y . Например,

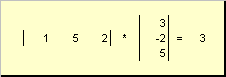
Рис. 14 Внутреннее (скалярное) произведение

Второе произведение

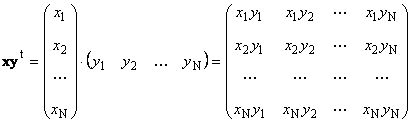
называется внешним . Его результат - это матрица размерности (N ×N ). Например,

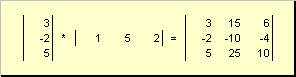
Рис. 15 Внешнее произведение

Векторы, скалярное произведение которых равно нулю, называются ортогональными .

1.9. Норма вектора

Скалярное произведение вектора самого на себя называется скалярным квадратом. Эта величина

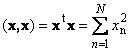
определяет квадрат длины вектора x . Для обозначения длины (называемой также нормой вектора) используется обозначение

Например,

Рис. 16 Норма вектора

Вектор единичной длины (||x || = 1) называется нормированным. Ненулевой вектор (x ≠ 0 ) можно нормировать, разделив его на длину, т.е. x = ||x || (x/ ||x ||) = ||x || e . Здесь e = x/ ||x || - нормированный вектор.

Векторы называются ортонормированными, если все они нормированы и попарно ортогональны.

1.10. Угол между векторами

Скалярное произведение определяет и угол φ между двумя векторами x и y

Если вектора ортогональны, то cosφ = 0 и φ = π/2, а если они колинеарны, то cosφ = 1 и φ = 0.

1.11. Векторное представление матрицы

Каждую матрицу A размера I ×J можно представить как набор векторов

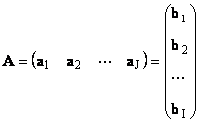
Здесь каждый вектор a j является j -ым столбцом, а вектор-строка b i является i -ой строкой матрицы A

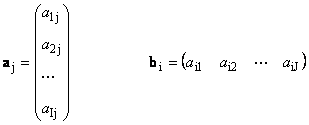
1.12. Линейно зависимые векторы

Векторы одинаковой размерности (N ) можно складывать и умножать на число, также как матрицы. В результате получится вектор той же размерности. Пусть имеется несколько векторов одной размерности x 1 , x 2 ,...,x K и столько же чисел α α 1 , α 2 ,...,α K . Вектор

y = α 1 x 1 + α 2 x 2 +...+ α K x K

называется линейной комбинацией векторов x k .

Если существуют такие ненулевые числа α k ≠ 0, k = 1,..., K , что y = 0 , то такой набор векторов x k называется линейно зависимым . В противном случае векторы называются линейно независимыми. Например, векторы x 1 = (2, 2) t и x 2 = (−1, −1) t линейно зависимы, т.к. x 1 +2x 2 = 0

1.13. Ранг матрицы

Рассмотрим набор из K векторов x 1 , x 2 ,...,x K размерности N . Рангом этой системы векторов называется максимальное число линейно-независимых векторов. Например в наборе

имеются только два линейно независимых вектора, например x 1 и x 2 , поэтому ее ранг равен 2.

Очевидно, что если векторов в наборе больше, чем их размерность (K >N ), то они обязательно линейно зависимы.

Рангом матрицы (обозначается rank(A )) называется ранг системы векторов, из которых она состоит. Хотя любую матрицу можно представить двумя способами (векторы столбцы или строки), это не влияет на величину ранга, т.к.

1.14. Обратная матрица

Квадратная матрица A называется невырожденной, если она имеет единственную обратную матрицу A -1 , определяемую условиями

AA −1 = A −1 A = I .

Обратная матрица существует не для всех матриц. Необходимым и достаточным условием невырожденности является

det(A ) ≠ 0 или rank(A ) = N .

Обращение матрицы - это сложная процедура, для выполнения которой существуют специальные программы. Например,

Рис. 17 Обращение матрицы

Приведем формулы для простейшего случая - матрицы 2×2

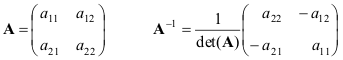
Если матрицы A и B невырождены, то

(AB ) −1 = B −1 A −1 .

1.15. Псевдообратная матрица

Если матрица A вырождена и обратная матрица не существует, то в некоторых случаях можно использовать псевдообратную матрицу, которая определяется как такая матрица A + , что

AA + A = A .

Псевдобратная матрица - не единственная и ее вид зависит от способа построения. Например для прямоугольной матрицы можно использовать метод Мура-Пенроуза .

Если число столбцов меньше числа строк, то

A + =(A t A ) −1 A t

Например,

Рис. 17a Псевдообращение матрицы

Если же число столбцов больше числа строк, то

A + =A t (AA t) −1

1.16. Умножение вектора на матрицу

Вектор x можно умножать на матрицу A подходящей размерности. При этом вектор-столбец умножается справа Ax , а вектор строка - слева x t A . Если размерность вектора J , а размерность матрицы I ×J то в результате получится вектор размерности I . Например,

Рис. 18 Умножение вектора на матрицу

Если матрица A - квадратная (I ×I ), то вектор y = Ax имеет ту же размерность, что и x . Очевидно, что

A (α 1 x 1 + α 2 x 2) = α 1 Ax 1 + α 2 Ax 2 .

Поэтому матрицы можно рассматривать как линейные преобразования векторов. В частности Ix = x , Ox = 0 .

2. Дополнительная информация

2.1. Системы линейных уравнений

Пусть A - матрица размером I ×J , а b - вектор размерности J . Рассмотрим уравнение

Ax = b

относительно вектора x , размерности I . По сути - это система из I линейных уравнений с J неизвестными x 1 ,...,x J . Решение существует в том, и только в том случае, когда

rank(A ) = rank(B ) = R ,

где B - это расширенная матрица размерности I ×(J+1 ), состоящая из матрицы A , дополненной столбцом b , B = (A b ). В противном случае уравнения несовместны.

Если R = I = J , то решение единственно

x = A −1 b .

Если R < I , то существует множество различных решений, которые можно выразить через линейную комбинацию J −R векторов. Система однородных уравнений Ax = 0 с квадратной матрицей A (N ×N ) имеет нетривиальное решение (x ≠ 0 ) тогда и только тогда, когда det(A ) = 0. Если R = rank(A )<N , то существуют N −R линейно независимых решений.

2.2. Билинейные и квадратичные формы

Если A - это квадратная матрица, а x и y - вектора соответствующей размерности, то скалярное произведение вида x t Ay называется билинейной формой, определяемой матрицей A . При x = y выражение x t Ax называется квадратичной формой.

2.3. Положительно определенные матрицы

Квадратная матрица A называется положительно определенной , если для любого ненулевого вектора x ≠ 0 ,

x t Ax > 0.

Аналогично определяются отрицательно (x t Ax < 0), неотрицательно (x t Ax ≥ 0) и неположительно (x t Ax ≤ 0) определенные матрицы.

2.4. Разложение Холецкого

Если симметричная матрица A положительно определена, то существует единственная треугольная матрица U с положительными элементами, для которой

A = U t U .

Например,

Рис. 19 Разложение Холецкого

2.5. Полярное разложение

Пусть A - это невырожденная квадратная матрица размерности N ×N . Тогда существует однозначное полярное представление

A = SR,

где S - это неотрицательная симметричная матрица, а R - это ортогональная матрица. Матрицы S и R могут быть определены явно:

S 2 = AA t или S = (AA t) ½ и R = S −1 A = (AA t) −½ A .

Например,

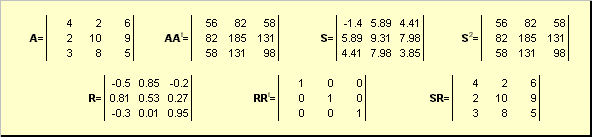
Рис. 20 Полярное разложение

Если матрица A вырождена, то разложение не единственно - а именно: S по-прежнему одна, а вот R может быть много. Полярное разложение представляет матрицу A как комбинацию сжатия/растяжения S и поворота R .

2.6. Собственные векторы и собственные значения

Пусть A - это квадратная матрица. Вектор v называется собственным вектором матрицы A , если

Av = λv ,

где число λ называется собственным значением матрицы A . Таким образом преобразование, которое выполняет матрица A над вектором v , сводится к простому растяжению или сжатию с коэффициентом λ. Собственный вектор определяется с точностью до умножения на константу α ≠ 0, т.е. если v - собственный вектор, то и αv - тоже собственный вектор.

2.7. Собственные значения

У матрицы A , размерностью (N ×N ) не может быть больше чем N собственных значений. Они удовлетворяют характеристическому уравнению

det(A − λI ) = 0,

являющемуся алгебраическим уравнением N -го порядка. В частности, для матрицы 2×2 характеристическое уравнение имеет вид

Например,

Рис. 21 Собственные значения

Набор собственных значений λ 1 ,..., λ N матрицы A называется спектром A .

Спектр обладает разнообразными свойствами. В частности

det(A ) = λ 1 ×...×λ N , Sp(A ) = λ 1 +...+λ N .

Собственные значения произвольной матрицы могут быть комплексными числами, однако если матрица симметричная (A t = A ), то ее собственные значения вещественны.

2.8. Собственные векторы

У матрицы A , размерностью (N ×N ) не может быть больше чем N собственных векторов, каждый из которых соответствует своему собственному значению. Для определения собственного вектора v n нужно решить систему однородных уравнений

(A − λ n I ) v n = 0 .

Она имеет нетривиальное решение, поскольку det(A − λ n I ) = 0.

Например,

Рис. 22 Собственные вектора

Собственные вектора симметричной матрицы ортогональны.

www.сайт позволяет найти . Сайт производит вычисление . За неколько секунд сервер выдаст правильное решение. Характеристическим уравнение для матрицы будет являться алгебраическое выражение, найденное по правилу вычисления определителя матрицы матрицы , при этом по главной диагонали будут стоять разницы значений диагональных элементов и переменной. При вычислении характеристического уравнения для матрицы онлайн , каждый элемент матрицы будет перемножаться с соответствующими другими элементами матрицы . Найти в режиме онлайн можно только для квадратной матрицы . Операция нахождения характеристического уравнения для матрицы онлайн сводится к вычислению алгебраической суммы произведения элементов матрицы как результат от нахождения определителя матрицы , только с целью определения характеристического уравнения для матрицы онлайн . Данная операция занимает особое место в теории матриц , позволяет найти собственные числа и векторы, используя корни . Задача по нахождению характеристического уравнения для матрицы онлайн заключается в перемножении элементов матрицы с последующим суммированием этих произведений по определенному правилу. www.сайт находит характеристическое уравнение для матрицы заданной размерности в режиме онлайн . Вычисление характеристического уравнения для матрицы онлайн при заданной её размерности - это нахождение многочлена с числовыми или символьными коэффициентами, найденного по правилу вычисления определителя матрицы - как сумма произведений соответствующих элементов матрицы , только с целью определения характеристического уравнения для матрицы онлайн . Нахождение полинома относительно переменной для квадратной матрицы , как определение характеристического уравнения для матрицы , распространено в теории матриц . Значение корней многочлена характеристического уравнения для матрицы онлайн используется для определения собственных векторов и собственных чисел для матрицы . При этом, если определитель матрицы будет равен нулю, то характеристическое уравнение матрицы все равно будет существовать, в отличии от обратной матрицы . Для того, чтобы вычислить характеристическое уравнение для матрицы или найти сразу для нескольких матриц характеристические уравнения , необходимо затратить не мало времени и усилий, в то время как наш сервер в считанные секунды найдет характеристическое уравнение для матрицы онлайн . При этом ответ по нахождению характеристического уравнения для матрицы онлайн будет правильным и с достаточной точностью, даже если числа при нахождении характеристического уравнения для матрицы онлайн будут иррациональными. На сайте www.сайт допускаются символьные записи в элементах матриц , то есть характеристическое уравнение для матрицы онлайн может быть представлено в общем символьном виде при вычислении характеристического уравнения матрицы онлайн . Полезно проверить ответ, полученный при решении задачи по нахождению характеристического уравнения для матрицы онлайн , используя сайт www.сайт . При совершении операции вычисления полинома - характеристического уравнения матрицы , необходимо быть внимательным и предельно сосредоточенным при решении данной задачи. В свою очередь наш сайт поможет Вам проверить своё решение на тему характеристическое уравнение матрицы онлайн . Если у Вас нет времени на долгие проверки решенных задач, то www.сайт безусловно будет являться удобным инструментом для проверки при нахождении и вычислении характеристического уравнения для матрицы онлайн .

СИСТЕМА ОДНОРОДНЫХ ЛИНЕЙНЫХ УРАВНЕНИЙ

Системой однородных линейных уравнений называется система вида

Ясно, что в этой случае , т.к. все элементы одного из столбцов в этих определителях равны нулю.

Так как неизвестные находятся по формулам , то в случае, когда Δ ≠ 0, система имеет единственное нулевое решение x = y = z = 0. Однако, во многих задачах интересен вопрос о том, имеет ли однородная система решения отличные от нулевого.

Теорема. Для того, чтобы система линейных однородных уравнений имела ненулевое решение, необходимо и достаточно, чтобы Δ ≠ 0.

Итак, если определитель Δ ≠ 0, то система имеет единственное решение. Если же Δ ≠ 0, то система линейных однородных уравнений имеет бесконечное множество решений.

Примеры.

СОБСТВЕННЫЕ ВЕКТОРЫ И СОБСТВЕННЫЕ ЗНАЧЕНИЯ МАТРИЦЫ

Пусть задана квадратная матрица , X – некоторая матрица–столбец, высота которой совпадает с порядком матрицы A . .

Во многих задачах приходится рассматривать уравнение относительно X

где λ – некоторое число. Понятно, что при любом λ это уравнение имеет нулевое решение .

Число λ, при котором это уравнение имеет ненулевые решения, называется собственным значением матрицы A , а X при таком λ называется собственным вектором матрицы A .

Найдём собственный вектор матрицы A . Поскольку E ∙X = X , то матричное уравнение можно переписать в виде или . В развёрнутом виде это уравнение можно переписать в виде системы линейных уравнений. Действительно .

И, следовательно,

Итак, получили систему однородных линейных уравнений для определения координат x 1 , x 2 , x 3 вектора X . Чтобы система имела ненулевые решения необходимо и достаточно, чтобы определитель системы был равен нулю, т.е.

Это уравнение 3-ей степени относительно λ. Оно называется характеристическим уравнением матрицы A и служит для определения собственных значений λ.

Каждому собственному значению λ соответствует собственный вектор X , координаты которого определяются из системы при соответствующем значении λ.

Примеры.

ВЕКТОРНАЯ АЛГЕБРА. ПОНЯТИЕ ВЕКТРОРА

При изучении различных разделов физики встречаются величины, которые полностью определяются заданием их численных значений, например, длина, площадь, масса, температура и т.д. Такие величины называются скалярными. Однако, кроме них встречаются и величины, для определения которых, кроме численного значения, необходимо знать также их направление в пространстве, например, сила, действующая на тело, скорость и ускорение тела при его движении в пространстве, напряжённость магнитного поля в данной точке пространства и т.д. Такие величины называются векторными.

Введём строгое определение.

Направленным отрезком назовём отрезок, относительно концов которого известно, какой из них первый, а какой второй.

Вектором называется направленный отрезок, имеющий определённую длину, т.е. это отрезок определённой длины, у которого одна из ограничивающих его точек принимается за начало, а вторая – за конец. Если A – начало вектора, B – его конец, то вектор обозначается символом, кроме того, вектор часто обозначается одной буквой . На рисунке вектор обозначается отрезком, а его направление стрелкой.

Модулем или длиной вектора называют длину определяющего его направленного отрезка. Обозначается || или ||.

К векторам будем относить и так называемый нулевой вектор, у которого начало и конец совпадают. Он обозначается . Нулевой вектор не имеет определенного направления и модуль его равен нулю ||=0.

Векторы и называются коллинеарными , если они расположены на одной прямой или на параллельных прямых. При этом если векторы и одинаково направлены, будем писать , противоположно .

Векторы, расположенные на прямых, параллельных одной и той же плоскости, называются компланарными .

Два вектора и называются равными , если они коллинеарны, одинаково направлены и равны по длине. В этом случае пишут .

Из определения равенства векторов следует, что вектор можно переносить параллельно самому себе, помещая его начало в любую точку пространства.

Например .

ЛИНЕЙНЫЕ ОПЕРАЦИИ НАД ВЕКТОРАМИ

1. Умножение вектора на число.

   Произведением вектора на число λ называется новый вектор такой, что:

   Произведение вектора на число λ обозначается .

   

   Например, есть вектор, направленный в ту же сторону, что и вектор , и имеющий длину, вдвое меньшую, чем вектор .

   Введённая операция обладает следующими свойствами :

2. Сложение векторов.

   Пусть и – два произвольных вектора. Возьмём произвольную точку O и построим вектор . После этого из точки A отложим вектор . Вектор , соединяющий начало первого вектора c концом второго , называется суммой этих векторов и обозначается .

   

   Сформулированное определение сложения векторов называют правилом параллелограмма , так как ту же самую сумму векторов можно получить следующим образом. Отложим от точки O векторы и . Построим на этих векторах параллелограмм ОАВС . Так как векторы , то вектор , являющийся диагональю параллелограмма, проведённой из вершины O , будет очевидно суммой векторов .

   

   Легко проверить следующие свойства сложения векторов .

3. Разность векторов.

   Вектор, коллинеарный данному вектору , равный ему по длине и противоположно направленный, называется противоположным вектором для вектора и обозначается . Противоположный вектор можно рассматривать как результат умножения вектора на число λ = –1: .